通讯作者:
收稿日期: 2018-05-5
修回日期: 2018-10-17
网络出版日期: 2019-02-20
版权声明: 2019 《地球信息科学学报》编辑部 《地球信息科学学报》编辑部 所有
基金资助:
作者简介:
作者简介:陈 动(1981-),男,山东临沂人,博士,主要从事机载激光点云的分类、分割、识别和重建研究。E-mail: chendong@njfu.edu.cn
展开
摘要
本文针对地基式激光雷达扫描点云的分布特征,提出一种基于骨架优化的三维树木重建方法。首先从原始点云中提取出树木的“类主干点”,利用无向图数据结构存储和组织点云,然后基于“主干点”约束下的最小生成树算法生成单株树木的初始骨架,最后通过“密度调整”和“树枝平滑”优化操作,建立高逼真度的三维树木模型。本文提出的树木几何重建算法对点云数据缺失和点云的密度不敏感,对试验区不同的树种建模具有较高的鲁棒性。另外,本文通过对不同密度的点云和不同抽稀层次下的点云进行效率测试,发现结合类主干点表达和点云抽稀能共同确保本文算法可以重建大场景TLS植被点云数据。
关键词:
Abstract
In this paper, we propose a methodology to reconstruct the individual-tree models from Terrestrial Laser Scanning (TLS) point clouds via skeleton-based optimization. The proposed method is a data-driven method, and in theory, it can generate any geometric shapes of different tree species. Mathematically, the salient points reflected from trunks and remarkable branches have been successfully recognized by using statistical analysis method. Then, we organize the raw points via an undirected graph, from which the initial skeleton of individual tree is created by using the Minimum Spanning Tree (MST) algorithm under the constraint of salient points. The initial skeleton tree models are further enhanced and refined through a series of optimizations, i.e., point density adjustment and branch smoothing. The tree skeletal structure is inflated into a tree model by simultaneous combination of a robust cylinder fitting method and allometric model. The tree leaves are finally properly added into the tree models, thereby enhancing the photorealistic representation of the geometric tree models. Various experiments on different tree species captured at Nanjing Forestry University show that the proposed methodology is insensitive to the point density and data missing, and meanwhile can generate meaningful and accurate individual geometric tree models. In addition, it is to be found that our modeling tree algorithm based on salient points and sampling strategy can reach the optimal computational efficiency, compared to that only using the salient points or the original laser scanning tree points as inputs. This enhancement in the efficiency can significantly expand our current individual tree modeling into the reconstruction of large-scale scanning scenes.
Keywords:
构建具有真实感的三维树木模型一直是计算机图形学、计算机视觉和遥感科学等领域研究的热点和难点问题。树木作为城市场景不可或缺的组成部分,精确重建三维树木模型有助于增强城市场景真实感,深化对城市场景的理解和认知。具有真实感的三维树木模型也是网络虚拟场景中最具有代表性的自然景观模型,其被广泛地应用于虚拟旅游、虚拟城市和虚拟生态景观模拟等领域[1]。另外,三维树木模型往往也是植被生态结构参数提取和反演的基础,定量化地描述树高、胸径、密度、蓄积量、碳储量和森林木材体积,甚至评估森林生态结构健康状况[2,3],都离不开三维树木几何模型的支持。地基式激光扫描(Terrestrial Laser Scanning,TLS)技术能够高密度、高精度地获取大面积树木的三维坐标和反射强度等信息,详细刻画树木的三维空间结构,为三维树木的几何重建提供了绝佳的遥感数据源[4],其被广泛应用于古建筑测量、遗产与文物保护、地质研究、建筑物施工、形变监测以及农林作物生长监测等领域[5]。基于上述背景,本文拟从含有噪声、离值点和数据缺失的TLS点云中重建高几何保真度和真实感的三维树木模型。
当前主流的树木建模方法分为基于树冠建模、基于语法结构建模和基于骨架建模3类。
(1)基于树冠的建模方法主要通过凸包算法来刻画整个树冠的几何形状[6,7],在树冠凸包内采用软件包,如PlantGL生成树枝[8]。该类方法主要关注树冠的整体几何形状,但无法精确地描述树冠内树枝的分布结构。基于树冠的建模通常用于茂盛树木的建模,或者对成片森林进行大尺度的三维重建,与其相关的深度应用并不关心树冠中树枝的具体形状和连接关系,仅要求相应的枝干符合一定的生成规律,从而构建具有全局几何一致性的三维树木模型。
(2)基于语法结构的建模L-system是生物学家Lindemayer[9]于1968年提出的模拟多细胞有机体生长的形式化体系,最初用于简单的多细胞有机体如藻类,根据其单个细胞的分裂、生长和死亡来进行有机体生长的建模。L-system随后被运用到高等植物和复杂树枝以及花序的建模。作为一种语法结构,L-system是对树木具有共性特征的一种描述,而现实中,往往由于树种的差异,树枝之间的几何形态和拓扑关系相差很大,特定的语法规则往往很难适应现实世界中变化多端的树木几何形态和树种类型。L-system更多被应用在已经建立完毕主要骨架结构的树模型的基础上,对其进行细枝和树叶的添加,增加模型视觉真实感。也就是说,如果能事先定义较为可靠的树枝生长语法规则,则可采用L-system对树木点云重建[9]。例如,Friedan等[11]通过小波分解树的结构,继而根据树结构重建树木的三维几何模型。为此,首先获得树的三维连接方式,然后采用三维小波变换,转化三维树结构到对应的小波系数空间,形成多尺度的三维树结构。根据一定的规则,确定小波系数空间中的三维树结构的使用方式,采用L-system语法结构获得一个完整的树模型。
(3)基于骨架的建模方法主要关注树枝的几何形状以及连接拓扑关系,树枝的伸展方式通过一个精细化的骨架结构表达。在获得初步骨架的基础上,再采用一系列优化方法对其进行改善,最后将优化过的骨架膨胀成树木的三维模型。例如,张天安等[12]耦合Dijkstra和线性规划优化方法,绘制出主要枝干的骨架;Wang等[13]则采用单站数据对具有数据缺失的树木点云提取骨架。马载阳等[13]基于B样条函数约束树干、树冠形态,依据削度方程模拟树干直径的变化趋势。Bucksch等[15]采用八叉树组织树木点云,即将三维空间中树木点云采用八叉树结构空间体素进行组织。通过设定一系列的规则对这些体素单元连接和合并产生骨架结构。虽然Bucksch等的方法具有线性时间复杂度,能快速从大规模的树木点云中生成稳定的骨架模型,且不受树干边界点云分布变化而产生额外树枝的影响,但是对点密度和亚采样具有敏感性,缺乏良好的几何细节。Vosselman[16]和Gorte[17]则通过首先栅格化树木点云,采用均匀栅格把一棵点云树变成栅格的树,然后对这些栅格采用形态学的方法进行缺失修复,最后采用Dijkstra算法来获得三维栅格的连接方式,进而得到一棵树的骨架结构。由于将点云转化成栅格再进行建模,因此获得骨架结构的精度严重受栅格尺寸的影响。Li等[18]提出一种利用TLS进行树木骨架建模的方法,该方法通过K-means聚类和反射强度分析得到输入点云,然后通过在无向图上实施深度优先搜索并结合一定的聚类算法生成骨架点,最后按照一定的拓扑将骨架点连接成树木骨架,通过拉普拉斯平滑得到最终三维模型。
综上说述,基于树冠的建模主要基于数据驱动进行宏观的尺度的重建,不过多地关注单株树木细枝的连接方式和拓扑关系,该方法较适合处理ALS(Airborne Laser Scanning)和UAV(Unmanned Aerial Vehicle)树木点云。基于语法结构的建模属于模型驱动建模的范畴,枝干的生长往往受限于特定的语法规则,枝干之间具有无误差的拓扑关系,虽然视觉表现上具有较强的真实感,但是整体的树木几何精度较低。相比上述2种方法,基于骨架的建模方法也是基于数据驱动思想,可构建更精细、真实的树木模型,特别适合处理TLS或MLS(Mobile Laser Scanning)三维点云数据。如果事先可将点云中单株植被精细分割,则很容易将该方法扩展到处理大规模树木的重建。因此,本文提出一种树木骨架优化下的TLS三维树木建模方法,通过对骨架进行精确的提取和后续的优化,能处理点云的数据缺失,降低算法对点云密度的敏感性,提高树木建模的鲁棒性。
本文针对TLS数据的特点,提出一种三维树木重建方法,如图1所示。首先从预处理完毕的树木点云中依据激光反射强度值的差异提取“类主干点”,采用最小生成树算法组织“类主干点”和剩余点,形成树的初步骨架并对骨架作进一步优化;然后在优化过的骨架上计算树枝半径并添加树叶;最后输出绘制好的三维树木几何模型。
图1 基于TLS树木建模的算法流程
Fig. 1 Methodological pipeline for skeleton-based tree modeling
本文首先对实验场景进行多站点扫描,扫描时合理布设标靶,利用标靶信息配准多站扫描数据,有效避免多株树木之间的遮挡和单株树木枝干之间自遮挡造成的数据缺失,从而保证扫描树木点云的完整性。在此基础上,本文进一步利用CloudCompare①(① http://www.cloudcompare.org/。) 商业软件,从扫描场景点云数据中手动分割单株树木,以此作为本文树木几何建模算法的输入。
树木骨架是构建三维树木模型的基础,本文着重阐述如何从地面激光点云中提取树木的初始骨架,进而优化初始骨架,最终实现树木骨架的提取。为此,首先依据激光反射强度值的差异,从预处理原始树木点云中,提取出树木的“类主干点”,然后采用图论中的“最小生成树”算法组织“类主干点”和剩余的“非主干点”,形成树木的初始骨架,最后通过“点密度调整”、“树枝平滑”对初始树木骨架进一步优化,得到比较精确且分布合理的树木骨架。
2.2.1 提取“类主干点”
由于树干、树冠细枝和树叶等的几何、材质显著不同,因此激光脉冲从树木不同部位得到的后向散射强度值(光谱)存在显著差异。据此,本文设计一种提取树木“类主干点”的方法,从原始树木点云中粗略区分出“类主干点”和“非主干点”。其中,“类主干点”主要指位于树主干和树冠中优势枝干上的点,而“非主干点”主要指位于树冠细枝和树叶上的点。“非主干点”往往对树木骨架提取构建起到干扰作用,因此为充分区分这两类点集,本文首先从预处理后的原始树木点云中,依据激光点云反射强度差异,采用“直方图统计分析”方法,通过实验得到经验阈值t,以有效区分“类主干点”和“非主干点”。由于对树木细枝缺乏严格意义上的定义,阈值t的设定也存在不确定性,所提取得到的“类主干点”不一定完全代表该株树木的“主干”,此时往往会产生树木“主干点”的过分割和欠分割现象,因此需要根据试验区不同树种的直方图统计,选择合适的阈值t,提取适合该类树种的“类主干点”和“非主干点”,详见第3节实验部分。
2.2.2 构建树木的粗略骨架
获得树木的“类主干点”以后,本文利用图论中最小生成树算法MST(Minimum Spanning Tree)组织“类主干点”和部分“非主干点”,形成树木的初始骨架。本文采用无向图G(V, E)组织点云,图的存储结构分为数组表示法、邻接表法、十字链表法、邻接多重表法。本文采用数组表示法存储点云,其中数组Vertex存储数据元素信息(即顶点),数组Edge存储数据元素之间的关系(即边)。本文提取出的“类主干点”中的每一个点作为图中的一个顶点,搜索每一个顶点周围最邻近的k个点,连接该点和这k个点形成边,并将每条边两顶点间的欧氏距离度量作为这条边的权重。考虑到单株树木点云数量较多,所建立的无向图为稠密图,本文采用Prim算法,从上述无向图中构建MST,从而提取树木的初始骨架。MST是一种所包含边的权重之和是所有生成树中边的权重之和最小的树组织形式。因此,要使权重之和最小,MST算法会优先连接短边,可以有效地描述区域内部主干点的连接关系。从无向图中融合MST提取的树木初始骨架的伪代码如表1所示。
表1 融合最小生成树算法的树木初始骨架生成伪代码
Tab. 1 The pseudocode for generating the initial tree skeleton
| 输入:一个非空的无向图G(V, E),V代表顶点集合,E代表边的集合。指定Zmin为根节点x 输出:Vnew和Enew描述了最小生成树的结构。 |
|---|
| 1 把根节点x添加到Vnew中,Vnew是最小生成树的点集,Vnew={x} 2 从V中移除根节点x 3 计算点i和点j之间边的权重eij 4 从V中选择到根节点x权重最小的一个点i,并且获得对应的边xi,添加点i到Vnew,添加边xi到Enew 5 For所有和点i相连的点,重新计算它们到最小生成树的权重 6 If一个点到最小生成树的权重大于这个点到点i的权重 7 Then把这个点到最小生成树的权重更新为这个点到点i的权重 8 这个点的连接方式变为和i点相连接 9 Else把这个点到最小生成树的权重不变 10 End If 11 从V中将i移除 12 End |
2.2.3 优化骨架
由于点云存在噪声、离值点和数据缺失,初始树木骨架中存在不少细枝与主干的连接错误,需要对得到的初步骨架进一步优化,得到反映真实树木几何外观且具有较高保真度的树木骨架,本文主要采用“点密度调整”和“树枝平滑”实现上述目标。
(1)点密度调整:点云的密度基于ε邻近图进行计算,ε邻近图的定义为:两点i-j之间具有相互连接的关系,如果j∈B(i; ε),其中B(i; ε)表示以i为中心以ε为欧式度量距离的原始点云的集合。基于ε邻近图组织原始树木点云,并根据式(1)计算点云的密度。
Di=N(B(i; ε))/ε (1)
式中:N(B(i; ε))表示ε邻近图中与i点直接连接的点的数目。本文ε取值为0.1 m,可较好地平衡点云的噪声和骨架的精度。如果ε取值过小,则树木的骨架会受到部分误分的类主干点的影响,使得所生成的枝干中会产生过多的毛刺,为后续树枝平滑带来一定的压力;相反ε取值过大,则会对骨架产生过渡抽象表达,从而损耗几何表达的精度。生成MST时,采用的是欧式距离作为边的权重,点云密度的变化会影响MST的连接方式,因此需要修改图 G(V, E)中边的权重。一般来说,一棵树的表面形态以及树枝伸展变化是连续且平滑的,例如在细小枝条的基础上很难生长出比其更加粗壮的枝条,相反,一根粗壮枝条具有较小的可能长出比它细小很多的枝条。根据这些特点,得到树点云的分布特征:① 在不存在数据缺失的情况下,MST上两点间的点云密度是相似的,在较小的范围内,点密度具有连续性且过渡平滑;② 树枝区域点密度大,说明该位置存在粗壮的树干的可能性较大,反之,该位置存在一些细枝或数据缺失的可能性较大。
基于上述点云分布性质,本文重新调整图G(V, E)中边的权重。首先修改无向图G(V, E)中每条边的权重,以适应点密度的变化。对应性质(i),相邻节点往往拥有相似的点密度,所以具有相似点密度节点间的权重小于非相似节点间的权重。对应性质(ii),优先连接点密度大的区域点云,继而判断点密度区域较小的点云是否与之连接,即要优先在具有较大点密度或相似点密度的区域构建树枝骨架。基于上述思想将会极大地降低由于树枝遮挡或自遮挡造成的数据缺失对生成树木骨架的敏感性,同时会使错综复杂的小枝对生成树木主干结构的影响显著降低,此时图G(V, E)中边的权重由式(2)决定。
eij=dij/(Di×Dj)×|Di-Dj| (2)
式中:Di和Dj分别是与点i和j相连的所有点组成的点集密度,dij是点i与j的欧式距离。一个点所在区域的点密度较大时,周围点到该点的距离就越小,反之就越大。i和j周围的点密度差距越大,|Di-Dj|差距就越大,边的权重eij越大;i和j周围的点密度差距越小,1/(Di×Dj)越大,边的权重eij就越大。式(2)很好地满足树点云分布的两条性质。
(2)树枝平滑。点密度调整以后树的骨架结构虽然得到了一定程度的调整,但是树枝的伸展方式并不自然,需要对这些树枝进行平滑,从而符合真实树枝的伸展方式。本文采用式(3)Laplacian方程对点云密度调整后的骨架进一步优化。
式中:WL和WH是对角矩阵,WL控制平滑的程度,WH控制平滑后的点云与原始点云相似的程度。WL中第i个对角元素的值定义成WL, i,WH中第i个对角元素的的值定义成WH,i。如果WL中的元素较大,那么平滑的程度较大;如果WH中的元素较大,平滑后的点云和原始点云相似度越高,平滑的程度越小。V是原始的点集,V '是优化过后的点集,L是n×n的拉普拉斯算子,通过式(4)定义:
式中:E表示骨架结构上的边的集合,i、j、k表示骨架结构上的点。将对角矩阵WL的对角线上的元素值设为一致,这样可以使每个点具有相同的收缩能力,或者说,有相同的平滑能力,本文中设为1。通过设置WH控制最后平滑的效果,矩阵WH对角线上的值是通过下述定义给出:
式中:k是i的父节点;j是i的子节点;θkij是∠kij。特别地,当点i表示的是末端点、根节点或交叉点时,将i单独设置成较大的值,使这几类点和原始点相比变化最小,因为这些点的位置基本没有变化,保持了树骨架原来的形状,并很好平滑了这些点中间的点。
2.3.1 半径计算
通过第2.2节提取得到最优树木骨架后,需要计算枝干的半径,从而利用OpenGL绘制具有真实感的三维树木几何模型。当前主流的计算枝干半径的方法主要有“圆柱拟合[19]”和“异速生长模型[20]”2类,本文充分耦合这2类方法,在树木枝干的精确性和不确定性方面取得平衡,从而实现对枝干半径的合理估算。
“圆柱体拟合法”的关键是确定圆柱体轴线的位置和方向以及圆柱体的半径。由于树木点云数据存在噪声、离值点,往往难以保证树枝局部范围内的所有点分布在一个圆柱体的表面。另外,由于树枝之间存在一定程度的遮挡和自遮挡,这使面对扫描仪方向的树木枝干获得的点云多,背对着扫描仪的方向枝干获得的点云较少,导致局部范围内树干点云难以拟合圆柱体。上述2个方面的缺陷共同导致基于数据驱动思想的“圆柱体拟合法”对树木点云质量具有极强的敏感性。“异速生长模型”主要通过异速生长理论,计算出骨架节点的半径,从而完成树干的重构。该方法需要提供较准确的树种和胸径等系列参数才有望构建具有较高逼真度和几何外观的三维树木模型。由于“异速生长模型”是基于模型驱动思想,同时耦合了特定树种的异速生长理论,因此得到的树木枝干半径是个近似值,其精度往往没有“圆柱体拟合法”高。
在现实中,如果点云扫描的质量较高,树干的半径可以用圆柱体拟合的方法来进行较为精确的估计,通过骨架结构上相邻2个点之间MST上所有点进行拟合。但是如果这些点分布不均匀,且存在大量噪声、离值点和数据缺失,采用圆柱体拟合难以获得良好的结果,此时“异速生长模型”则为估算树枝半径提供了一种替代方案。基于上述分析,本文结合“圆柱体拟合”和“异速生长模型”共同确定骨架结构上每一点对应的半径。具体而言,分别采用“圆柱体拟合”和“异速生长模型”计算构架结构上某一特点pi的半径,结果分别为ric和ria,然后检查ric是否满足如式(6),如果满足,则令ric为当前点 pi的真值半径。该过程计算完成后,本文采用式(7)[13]计算骨架上其它未知点的半径。该式用已知点的真值半径作为正则项,采用“异速生长模型”构建约束项,具体定义如下。
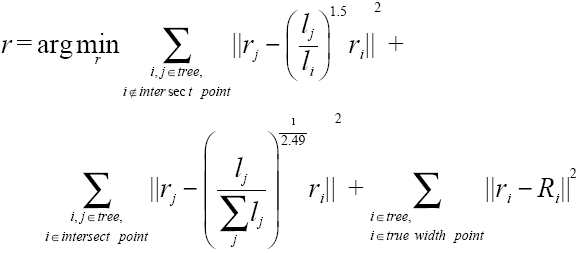
式中:i和j是骨架结构上的点,且j为i的子节点;li和lj是i和 j所有后向支持边的总和;Ri是i存在真值的情况下,该点的真值;ri和rj分别是i和j点的最终半径;r={r1, r2, …},通过求解式(7)获得每一个节点的半径。
2.3.2 添加树叶
获得每一节点的半径后,骨架模型膨胀成三维树模型,就构建完成了一棵没有叶子的树木三维几何模型。通常情况下,如果一棵树存在叶子,叶子位于点密度相对较高,但半径却相对较小的位置的可能性较高。为了识别这些位置,针对每一个节点,根据式(8)判断该节点是否存在叶子。
Gi=Di/ri (8)
式中:ri代表每个节点的半径;Di是与i点相连的所有点的点云密度。从式(8)可知,半径小的时候Gi大,密度大的时候Gi大,所以Gi用于判断节点i是否存在叶子。所有节点获得了对应的Gi值后,对这些值从大到小排序。设定一个百分比的阈值控制整棵树存在叶子节点的比例,如前30%(经验参数)的点存在叶子节点。获得这些点的位置以后,在这些点上随机加上一些叶子,就建立了一棵完整的三维树模型。
本次实验仪器为瑞士徕卡Leica ScanStation C10三维激光扫描仪,如图2(a)所示,仪器参数如表2所示。本次实验区为南京林业大学校园,数据获取时间为2017年初,在扫描过程中配有6个标靶,用于站点配准及拼接。本次实验选用Leica ScanStation C10三维激光扫描仪配备的后处理软件Cyclone对实验区的各站点数据进行拼接匹配,形成完整的实验场景,如图3所示。本文拼接和匹配仅仅是为了尽可能保证单株树木扫描点云的完整性。根据表2激光扫描仪的指标,在50 m的扫描距离内,扫描点的水平精度为6 mm 测距精度为 4 mm。本文选择的实验树木基本都分布在以扫描仪为中心的半径为100 m的距离范围内,根据单株树木的尺寸及其所设置的扫描线的分辨率不同,拼接后每株树木的点云在几千到几十万个不等。
图2 Leica ScanStation C10三维激光扫描仪和标靶
Fig. 2 Leica ScanStation C10 scanner and its corresponding flat calibration target
图3 南京林业大学两站TLS数据拼接后的场景
Fig. 3 Two registered scanning scenes at Nanjing Forestry University
表2 Leica ScanStation C10仪器参数
Tab. 2 The detailed parameters for Leica ScanStation C10 TLS scanner
| 指标 | 参数 |
|---|---|
| 类型 激光颜色 测程 扫描速率 扫描分辨率 视场 瞄准/视域 | 脉冲式;专用微芯片 绿色;可见(波长为532 nm)300 m@90%;134 m@18% albedo(最小距离为0.1 m) 最大50 000点/s 激光点的位置:≤6 mm 在0~50 m内(基于高斯定义) ≤4 mm 在0~50 m内(基于FWHH定义) 水平:360°(最大);竖直:270°(最大) 全景内置摄像头 |
本文重点研究基于树木点云的三维重建,对实验区的道路、建筑、标杆、路灯等地物不作考虑,故需要从大场景中利用Cloudcompare开源软件包,手动裁剪出单株完整树木点云。从图3中选取不同树种的多棵树木作为本文算法的输入。
反射强度值的大小与树木的种类、表面粗糙度、距离扫描仪的远近有关。从校园扫描场景中选取30株样本树木,采用直方图统计分析,统计激光反射强度阈值,如表3(见第243页)所示。由表3可知,30株不同树种的树木的最佳反射强度阈值τ变化较小,这主要取决于树木枝干这种材质的反射率,树种不同,相应枝干的几何特征、枝干表面的粗糙度也略有不同,这就造成了最佳反射强度阈值τ的略微差异。另外,两站实验数据中所选择的30株树木与扫描仪之间的距离都近似,大约分布在以扫描仪为中心的100 m半径范围内,这导致了反射强度具有相同的数量级,即激光脉冲在扫描距离的衰减率上可以近似认为具有一致性。
表3 校园内30株样本树木激光反射强度阈值τ的选取情况
Tab. 3 The reflected intensity thresholds for 30 representative trees
| 序号 | τ阈值 | 序号 | τ阈值 | 序号 | τ阈值 |
|---|---|---|---|---|---|
| 1 | 5348 | 11 | 5417 | 21 | 5212 |
| 2 | 5169 | 12 | 5098 | 22 | 5207 |
| 3 | 5407 | 13 | 5279 | 23 | 5179 |
| 4 | 5011 | 14 | 4996 | 24 | 5348 |
| 5 | 5139 | 15 | 5087 | 25 | 5418 |
| 6 | 5289 | 16 | 5200 | 26 | 5366 |
| 7 | 5043 | 17 | 5368 | 27 | 5201 |
| 8 | 5399 | 18 | 5371 | 28 | 5206 |
| 9 | 5015 | 19 | 5208 | 29 | 5311 |
| 10 | 5222 | 20 | 5402 | 30 | 5182 |
利用反射强度直方图找到使得反射强度分布产生近似跳跃变化的拐点,以此作为典型阈值τ下的类主干点。如图4,借助直方图的指导,展示了在不同阈值τ下3棵不同树种的树木“类主干点”的差异。3棵树木直方图都近似服从正态分布,比较理想τ值的选择,应处于正态分布的上升沿所处的微小区间内,具体的数值根据树种的不同略有差异。图4中每棵树种对应的直方图中,红线对应的阈值τ可以较好地描述树木的枝干,这些枝干点组成了MST构建树木骨架的基础,减少了“非主干点”对树木骨架构建的干扰。另外,基于“类主干点”重构树木三维模型也极大地缩减了参与运算的点云数量,提高了建模的效率。
图4 基于直方图统计下的“类主干点”提取示例注:红色表示“类主干点”,绿色表示“非主干点”。
Fig. 4 Examples of "Class Trunk Points" extraction based on histogram statistics
提取到“类主干点”后根据表1算法,构建融合最小生成树和类骨架点的树木初始骨架,如图5所示。通过观察可以发现,树木初始骨架可以基本上反映原始点云中树木的枝干趋势,即便在红色矩形区域出现了点云数据的缺失,利用本文的最小生成树算法也可以将缺失数据的骨架补齐。
虽然图5(b)可以大体反映原始点云的宏观趋势,但与初始骨架的对比发现,不少细枝与主干的连接存在错误,需优化和调整初始骨架,从而更合理地反映树木细枝的连接拓扑。本文采用第2.2.3节点密度调整策略,消除一些连接错误的细枝。调整前后的结果如图6所示,调整后红色方框内的细枝分布更均匀。另外,实施拉普拉斯平滑操作后,树枝的伸展方式更自然,从而更符合真实场景中树枝的伸展方式。图7(a)为考虑点云密度后的优化结果,图7(b)为再次实施拉普拉斯平滑后的结果,图7(b)红色方框内的细节平滑后走势更自然。
图6 点密度调整前后对比
Fig. 6 The skeleton comparison before and after density adjustment
通过对骨架半径计算和添枝加叶后可得到完整的树木模型。如图8所示,对图4中裁剪的3棵不同树种的树木,构建三维树木模型。图8(a1)-图8(a4)所示树木位于南京林业大学教五楼正门前,整棵树点云基本完整,只在底部存在少量的数据缺失,这部分数据缺失是由于扫描时行人遮挡造成的。从视觉上重建的树模型和点云中的树基本一致,树枝的结构和伸展方式都得到了保持。虽然因为行人遮挡造成了一些轻微的点云缺失,但是基本没有影响整体的建模效果。图8(b1)- 图8(b4)树木位于南京林业大学图书馆后,整体建模效果较好,树木模型的伸展方式基本符合树木点云的伸展方式,由于该株树木的底部存在木棍的支撑,在建模时手动去掉木棍点云,因此在木棍交叉处的建模效果略有变形。图8(c1)-图8(c4)所示树木位于南京林业大学学术报告厅门前,整棵树点云基本完整,底部存在少量的数据缺失,但对树木模型构建的影响不大,从视觉上重建的树模型和点云中的树基本一致,树枝的结构和伸展方式都得到了保持。
图8 3类树种的模型重建注:图(a1)-(c1)树的原始点云;图(a2)-(c2)树骨架;图(a3)-(c3)树模型;图(a4)-(c4)添加树叶的树木模型。
Fig. 8 Reconstruction of three species of trees
3.3.1 鲁棒性分析
为了证明本文方法对点云密度有好的适应性,本文对原始树木点云随机抽稀重采样,用抽稀后的点云进行建模,以评价树木建模算法的鲁棒性。具体而言,采用原始树木点云的100%,70%,50%以及30%的点云进行建模,图9(见第247页)显示了不同点密度下两棵树建模结果。从图9可知,虽然点云密度差距较大,但是每组中4棵树模型的结构是相似的,主要细枝结构得到了很好的保持。虽然大量的点云移除会影响树木细枝的连接关系,如在红色矩形框内由于原始点云数量相对比较稀少,在随机抽稀后这部分点云数量急剧减少,甚至完全丢失,造成该区域连接关系发生变化,但是总体结构上的相似性,间接说明了本文方法对点密度的变化具有鲁棒性。需要说明的是,点云抽稀会影响点密度的计算,随着抽稀力度的增加,ε的取值相应的也要增加。本文中采用原始树木点云100%、70%、50%以及30%时对应的ε值分别设置为:0.1、0.2、0.3和0.5 m,可较好地平衡树木三维模型的抽象表达和树木模型的几何精度之间的关系。
图9 经过抽稀后的树木点云建模 注:本文通过对原始点云进行抽稀,测试树木模型重建算法对点云密度的敏感性,即分别利用100%、70%、50%和30%的原始点云对算法进行测试,图中最左列至最右列依次对应树木重建的结果。
Fig. 9 The reconstructed tree models using the different density of point clouds
3.3.2 建模效率分析
为了进一步验证本文算法的效率,从表3中任意选择10株树木,分3种情形评价建模算法的效率:情形(a):将单株树木的所有点都作为类主干点进行建模;情形(b):每株树木采用类主干点进行建模;情形(c):每株树木抽稀70%后,再进行类主干点建模。每种情形多株植被累加的计算时间如图10(见第247页)所示。图10中的耗时是在Release模式下,硬件配置为2.70 GHz Intel(R) Core(TM) i7-6820HQ CPU, 8 GB 内存,HD Graphics 530 GPU计算得到的。从图4可看出,类主干点优化相比原始点云植被建模,平均可提升约2倍的计算效率,在此基础上通过点云的抽稀可进一步提升计算效率,因此,基于结合类主干点骨架优化和点云抽稀的方法共同保证本文算法可以应用于处理大场景TLS植被点云数据。
图10 3种情形下的树木建模效率分析
Fig. 10 Comparisons of computational efficiency among three different situations
本文提出一种基于骨架优化的三维树木建模方法,针对地基式激光扫描点云数据的特点,首先从原始树木点云中提取出“类主干点”,利用无向图的方式存储和组织点云,然后基于最小生成树算法形成树木骨架,最后在经过一系列优化后的骨架上构建较准确的三维树木模型。本文提出的先提取“类主干点”再进行骨架优化的方法能提高骨架生成的效率,对较小的数据缺失和噪声不敏感,既能灵活地适应树枝的伸展方向,又能良好地描述树枝的细节,在散乱的树冠点云中,避免了树的主干部分的连接方式受细小的树枝影响。另外,在单站式地面激光扫描数据一般存在大量的缺失和点密度极其不均质的分布特征情形下,利用此类树木点云数据进行建模是一项具有挑战性的工作,而本文可以处理点云缺失数据,在一定程度上可缓解由于单站扫描对树木建模带来的挑战。本文目前的骨架优化仅仅融合了点云密度调整和平滑树枝2个方面的内容,针对由于严重数据缺失造成局部骨架连接错误的问题,今后需进一步探索如何先填补严重缺失部位的点云,然后在缺失数据添补过后点云的基础上再优化树木骨架,从而构建更精准的三维树木模型。
The authors have declared that no competing interests exist.
| [1] |
3D数据建模技术研究进展 [J].Survey on virtual 3D tree modeling technologies [J]. |
| [2] |
基于TLS数据的单木胸径和树高提取研究 [J].
利用TLS测量森林参数(树高、胸径和林分密度等)不仅节省人力,而且还能提高工作效率,目前已成为快速获取树木几何参数的有效方法之一。本文利用地基激光雷达数据,提出了一种半自动方式提取单木参数的方法。首先,利用发射脉冲与接收回波脉冲的形状偏差和强度对原始点云数据中的"飞点"和噪点进行滤除;然后,配准各站点云数据;接下来采用不同目标回波过滤方法滤除部分树叶点和其他非树干点;抽稀、合并各站点云数据,对合并后的点云数据水平分层并生成对应的灰度影像;对灰度影像采用Hough变换方法估测单木位置和胸径;对Hough变换检测层数较少的结果采用椭圆拟合方法重新检测;最后,结合Hough变换和椭圆拟合检测结果从点云数据中提取单木位置、胸径和树高。用小兴安岭凉水自然保护区的白桦天然次生林对算法进行了检验,5块多站扫描样地单木识别的平均精度为72.16%,将所提取的单木位置、胸径和树高与外业实际测量数据对比,结果一致性较高。5块多站扫描样地的胸径和树高均方根误差分别为2.38、2.55、3.58、2.21、1.92cm和4.31、3.87、2.34、5.00、3.47m。
Extraction of individual tree DBH and height based on terrestrial laser scanner data [J].
利用TLS测量森林参数(树高、胸径和林分密度等)不仅节省人力,而且还能提高工作效率,目前已成为快速获取树木几何参数的有效方法之一。本文利用地基激光雷达数据,提出了一种半自动方式提取单木参数的方法。首先,利用发射脉冲与接收回波脉冲的形状偏差和强度对原始点云数据中的"飞点"和噪点进行滤除;然后,配准各站点云数据;接下来采用不同目标回波过滤方法滤除部分树叶点和其他非树干点;抽稀、合并各站点云数据,对合并后的点云数据水平分层并生成对应的灰度影像;对灰度影像采用Hough变换方法估测单木位置和胸径;对Hough变换检测层数较少的结果采用椭圆拟合方法重新检测;最后,结合Hough变换和椭圆拟合检测结果从点云数据中提取单木位置、胸径和树高。用小兴安岭凉水自然保护区的白桦天然次生林对算法进行了检验,5块多站扫描样地单木识别的平均精度为72.16%,将所提取的单木位置、胸径和树高与外业实际测量数据对比,结果一致性较高。5块多站扫描样地的胸径和树高均方根误差分别为2.38、2.55、3.58、2.21、1.92cm和4.31、3.87、2.34、5.00、3.47m。
|
| [3] |
生长模型驱动的单株杉木三维动态模拟 [J].https://doi.org/10.3724/SP.J.1047.2015.00668 URL Magsci [本文引用: 1] 摘要
<p>虚拟植物是一种潜在、有力的植物分析辅助工具, 而单株木生长模拟是森林生态系统模拟的基础。为了动态模拟杉木生长发育过程, 提出了参数化单株木三维形态结构建模和与距离无关的单木生长模型的集成方法, 其主要过程为:首先, 根据杉木的形态结构特征, 采用参数化建模方法建立特定生长阶段的三维静态模型;其次, 根据生长模型预测不同年龄杉木的树高、胸径、枝下高和分枝轮数, 并与树木三维静态模型几何描述参数建立联动;最后, 采用参数曲线调整干径和枝径变化、枝条长度、分枝角等形态结构参数, 使模型形态随树龄增长而变化。在自主研发的ParaTree系统上, 扩展杉木动态生长模拟模块, 并以福建省漳平五一林场的二类调查数据为例, 动态模拟了杉木的生长过程。模拟结果表明, 本方法可直观表达林分中林木个体平均生长状况和大体形态结构特征。树木三维模型描述参数与传统树木统计生长模型结合, 有利于重用林业领域淀积大量的生长模型。</p>
Growth model driven individual tree 3D dynamic simulation of cunninghamia lanceolata [J].https://doi.org/10.3724/SP.J.1047.2015.00668 URL Magsci [本文引用: 1] 摘要
<p>虚拟植物是一种潜在、有力的植物分析辅助工具, 而单株木生长模拟是森林生态系统模拟的基础。为了动态模拟杉木生长发育过程, 提出了参数化单株木三维形态结构建模和与距离无关的单木生长模型的集成方法, 其主要过程为:首先, 根据杉木的形态结构特征, 采用参数化建模方法建立特定生长阶段的三维静态模型;其次, 根据生长模型预测不同年龄杉木的树高、胸径、枝下高和分枝轮数, 并与树木三维静态模型几何描述参数建立联动;最后, 采用参数曲线调整干径和枝径变化、枝条长度、分枝角等形态结构参数, 使模型形态随树龄增长而变化。在自主研发的ParaTree系统上, 扩展杉木动态生长模拟模块, 并以福建省漳平五一林场的二类调查数据为例, 动态模拟了杉木的生长过程。模拟结果表明, 本方法可直观表达林分中林木个体平均生长状况和大体形态结构特征。树木三维模型描述参数与传统树木统计生长模型结合, 有利于重用林业领域淀积大量的生长模型。</p>
|
| [4] |
基于地面三维激光扫描的树木枝干建模与参数提取技术[D] .Branches Modeling and Morphological Parameters Extraction Technology Based on 3D Laser Scanning Technology[D] . |
| [5] |
地基激光雷达在森林参数反演上的应用 [J].https://doi.org/10.3969/j.issn.1672-5867.2011.06.017 URL [本文引用: 1] 摘要
In recent years, terrestrial laser scanning (TLS) has been rapidly developed. It can quickly obtain high-precision and high-density 3D point clouds, and can be applied in the fields of engineering, forestry, agriculture, mining, transportation, urban planning and heritage records. Using the TLS to measure forest parameters (tree height, DBH, tree density and volume, etc) for quantitative survey not only saves manpower, but also improves work efficiency, which has been a fast and effective way to obtain geometric parameters of trees now. This paper introduced the working principle of TLS, the process and methods of data processing, the application status in forestry sector, the methods of retrieving forest parameters (positions, DBH, tree height, volume, stem, canopy cover, etc), reviewed the research progress using TLS, and made analysis and prospect in future TLS application in forestry sector.
A review of TLS application in forest parameters retrieving [J].https://doi.org/10.3969/j.issn.1672-5867.2011.06.017 URL [本文引用: 1] 摘要
In recent years, terrestrial laser scanning (TLS) has been rapidly developed. It can quickly obtain high-precision and high-density 3D point clouds, and can be applied in the fields of engineering, forestry, agriculture, mining, transportation, urban planning and heritage records. Using the TLS to measure forest parameters (tree height, DBH, tree density and volume, etc) for quantitative survey not only saves manpower, but also improves work efficiency, which has been a fast and effective way to obtain geometric parameters of trees now. This paper introduced the working principle of TLS, the process and methods of data processing, the application status in forestry sector, the methods of retrieving forest parameters (positions, DBH, tree height, volume, stem, canopy cover, etc), reviewed the research progress using TLS, and made analysis and prospect in future TLS application in forestry sector.
|
| [6] |
Reconstruction of tree crown shape from scanned data [C]. |
| [7] |
Tree modelling from mobile laser scanning data-sets[R] . |
| [8] |
PlantGL: A pythonbased geometric library for 3D plant modelling at different scales [J].https://doi.org/10.1016/j.gmod.2008.10.001 URL [本文引用: 1] 摘要
In this paper, we present PlantGL, an open-source graphic toolkit for the creation, simulation and analysis of 3D virtual plants. This C++ geometric library is embedded in the Python language which makes it a powerful user-interactive platform for plant modeling in various biological application domains. PlantGL makes it possible to build and manipulate geometric models of plants or plant parts, ranging from tissues and organs to plant populations. Based on a scene graph augmented with primitives dedicated to plant representation, several methods are provided to create plant architectures from either field measurements or procedural algorithms. Because they are particularly useful in plant design and analysis, special attention has been paid to the definition and use of branching system envelopes. Several examples from different modelling applications illustrate how PlantGL can be used to construct, analyse or manipulate geometric models at different scales ranging from tissues to plant communities.
|
| [9] |
Mathematical models for cellular interactions in development, Parts I and II [J].https://doi.org/10.1016/0022-5193(68)90079-9 URL [本文引用: 2] |
| [10] |
树的建模技术研究综述与展望 [J].https://doi.org/10.3969/j.issn.1002-137X.2010.06.004 URL 摘要
树的建模技术是计算机图形学近年来研究的热点问题之一。侧重从计算机图形学的研究角度,对树的建模技术分别从基于规则的树建模技术、基于草图的树建模技术、基于图像的树建模技术3个方面进行了总结和综述,介绍了近年来提出的典型的树建模方法及最新研究进展,对其中涉及的关键技术进行了总结分析,给出了这些技术的基本思想、局限性和使用范围,并加以分析比较,最后对树的建模技术的未来研究方向给出展望。
Review and prospect of tree modeling techniques [J].https://doi.org/10.3969/j.issn.1002-137X.2010.06.004 URL 摘要
树的建模技术是计算机图形学近年来研究的热点问题之一。侧重从计算机图形学的研究角度,对树的建模技术分别从基于规则的树建模技术、基于草图的树建模技术、基于图像的树建模技术3个方面进行了总结和综述,介绍了近年来提出的典型的树建模方法及最新研究进展,对其中涉及的关键技术进行了总结分析,给出了这些技术的基本思想、局限性和使用范围,并加以分析比较,最后对树的建模技术的未来研究方向给出展望。
|
| [11] |
Automatic procedural modeling of tree structures in point clouds using wavelets [C]. |
| [12] |
基于骨架提取的树木主枝干三维重建算法 [J].https://doi.org/10.3969/j.issn.1672-1292.2014.04.009 URL [本文引用: 1] 摘要
为了实现树木主枝干的三维重建,提出了一种基于骨架提取的算法.首先,根据Dijkstra距离对点云数据进行分段.然后,提取出每个连通部分的骨架,并采用线性规划的优化模型求出距离与角度的权值,根据加权后的匹配度进行骨架的连接,得到整株树的完整骨架.最后利用圆柱体拟合出树木枝干的模型,对含笑树和樱花树分别进行了实验,得到了令人满意的实验结果.
Three-dimensional reconstruction algorithm of tree limbs based on skeleton extraction [J].https://doi.org/10.3969/j.issn.1672-1292.2014.04.009 URL [本文引用: 1] 摘要
为了实现树木主枝干的三维重建,提出了一种基于骨架提取的算法.首先,根据Dijkstra距离对点云数据进行分段.然后,提取出每个连通部分的骨架,并采用线性规划的优化模型求出距离与角度的权值,根据加权后的匹配度进行骨架的连接,得到整株树的完整骨架.最后利用圆柱体拟合出树木枝干的模型,对含笑树和樱花树分别进行了实验,得到了令人满意的实验结果.
|
| [13] |
A structure-aware global optimization method for reconstructing 3-d tree models from terrestrial laser scanning data [J].https://doi.org/10.1109/tgrs.2013.2291815 URL [本文引用: 3] 摘要
A 3-D tree structure plays an important role in many scientific fields, including forestry and agriculture. For example, terrestrial laser scanning (TLS) can efficiently capture high-precision 3-D spatial arrangements and structure of trees as a point cloud. In the past, several methods to reconstruct 3-D trees from the TLS point cloud were proposed. However, in general, they fail to process incomplete TLS data. To address such incomplete TLS data sets, a new method that is based on a structure-aware global optimization approach (SAGO) is proposed. The SAGO first obtains the approximate tree skeleton from a distance minimum spanning tree (DMst) and then defines the stretching directions of the branches on the tree skeleton. Based on these stretching directions, the SAGO recovers missing data in the incomplete TLS point cloud. The DMst is applied again to obtain the refined tree skeleton from the optimized data, and the tree skeleton is smoothed by employing a Laplacian function. To reconstruct 3-D tree models, the radius of each branch section is estimated, and leaves are added to form the crown geometry. The developed methodology has been extensively evaluated by employing a dozen TLS point clouds of various types of trees. Both qualitative and quantitative performance evaluation results have indicated that the SAGO is capable of effectively reconstructing 3-D tree models from grossly incomplete TLS point clouds with significant amounts of missing data.
|
| [14] |
林木多样性模型及生长模拟 [J].URL 摘要
林木生存环境复杂多变,导致林木形态千差万别,为了准确描述林木的形态多样性特征,提出了一种基于模型分解的林木生长模拟方法。首先构建多样性林木三维模型,使用林木形态的实际测量数据,基于B样条函数约束树干、树冠形态,依据削度方程模拟树干直径的变化趋势,利用Direct3D实现林木形态的三维建模;其次,按林木形态特征进行林木模型分解,将林木模型分为9个子模型;最后,使用场景节点按照拓扑结构关系对子模型进行动态组织,基于胸径、树高、枝下高、冠高和冠幅生长模型,使用多核CPU多线程并行的计算方式,获得各年龄阶段林木东、南、西、北方向形态参数,从而对子模型生长状态进行控制,实现林木不同方向生长变化的可视化模拟。结果表明:该方法可将林木三维模型与生长模型紧密结合起来,林木各方向的枝下高、冠高和冠幅严格按照生长模型进行生长,可有效模拟出林木各方向生长状态的多样性;三维场景渲染帧率(FPS)保持在25以上,平均FPS可以达到50,实现林木生长的方向异质性模拟。
Diversity model and growth simulation of tree [J].URL 摘要
林木生存环境复杂多变,导致林木形态千差万别,为了准确描述林木的形态多样性特征,提出了一种基于模型分解的林木生长模拟方法。首先构建多样性林木三维模型,使用林木形态的实际测量数据,基于B样条函数约束树干、树冠形态,依据削度方程模拟树干直径的变化趋势,利用Direct3D实现林木形态的三维建模;其次,按林木形态特征进行林木模型分解,将林木模型分为9个子模型;最后,使用场景节点按照拓扑结构关系对子模型进行动态组织,基于胸径、树高、枝下高、冠高和冠幅生长模型,使用多核CPU多线程并行的计算方式,获得各年龄阶段林木东、南、西、北方向形态参数,从而对子模型生长状态进行控制,实现林木不同方向生长变化的可视化模拟。结果表明:该方法可将林木三维模型与生长模型紧密结合起来,林木各方向的枝下高、冠高和冠幅严格按照生长模型进行生长,可有效模拟出林木各方向生长状态的多样性;三维场景渲染帧率(FPS)保持在25以上,平均FPS可以达到50,实现林木生长的方向异质性模拟。
|
| [15] |
Campino-A skeletonization method for point cloud processing [J].https://doi.org/10.1016/j.isprsjprs.2007.10.004 URL [本文引用: 1] 摘要
A new algorithm for deriving skeletons and segmentations from point cloud data in () time is explained in this publication. This skeleton is represented as a graph, which can be embedded into the point cloud. The CAMPINO method, (C)ollapsing (A)nd (M)erging (P)rocedures (IN) (O)ctree-graphs, is based on cycle elimination in a graph as derived from an octree based space division procedure. The algorithm is able to extract the skeleton from point clouds generated from either one or multiple viewpoints. The correspondence between the vertices of the graph and the original points of the point cloud is used to derive an initial segmentation of these points. The principle of the algorithm is demonstrated on a synthetic point cloud consisting of 3 connected tori. Initially this algorithm was developed to obtain skeletons from point clouds representing natural trees, measured with the terrestrial laser scanner IMAGER 5003 of Zoller+Fr枚hlich. The results show that CAMPINO is able to automatically derive realistic skeletons that fit the original point cloud well and are suited as a basis for e.g. further automatic feature extraction or skeleton-based registration.
|
| [16] |
3D reconstruction of roads and trees for city modeling [J]. |
| [17] |
Skeletonization of laser-scanned trees in the 3D raster domain [C]. |
| [18] |
An automatic tree skeleton extracting method based on point cloud of terrestrial laser scanner [J]. |
| [19] |
圆柱体的拟合与质量检测 [J].https://doi.org/10.13474/j.cnki.11-2246.2014.0123 URL [本文引用: 1] 摘要
为检测空间圆柱体的位置和形态变化,利用无反射电子全站仪观测圆柱体外表面上均匀分布的若干点位,将不同测站上观测的点位坐标通过公共点归算到同一坐标系下,根据观测点的三维坐标,选择合适的方法拟合出圆柱体的空间位置参数和形状参数。本文介绍一种基于最小二乘原理的空间圆柱体拟合方法,详细阐述圆柱体质量检测的原理与计算过程,并通过算例验证了该圆柱体拟合方法的正确性与可靠性,以及质量检测方法的可行性。
The fitting and quality testing of cylinder [J].https://doi.org/10.13474/j.cnki.11-2246.2014.0123 URL [本文引用: 1] 摘要
为检测空间圆柱体的位置和形态变化,利用无反射电子全站仪观测圆柱体外表面上均匀分布的若干点位,将不同测站上观测的点位坐标通过公共点归算到同一坐标系下,根据观测点的三维坐标,选择合适的方法拟合出圆柱体的空间位置参数和形状参数。本文介绍一种基于最小二乘原理的空间圆柱体拟合方法,详细阐述圆柱体质量检测的原理与计算过程,并通过算例验证了该圆柱体拟合方法的正确性与可靠性,以及质量检测方法的可行性。
|
| [20] |
异速生长法计算秋茄红树林生物量 [J].https://doi.org/10.5846/stxb201105160634 URL Magsci [本文引用: 1] 摘要
采用异速生长方法,建立树干基部多分枝型秋茄生物量与分枝直径的函数模型,根据该模型计算了浙江鳌江河口人工秋茄林生物量,并比较了我国不同地区秋茄林生物量差异。结果表明,秋茄生物量(<em>W</em>)与分枝直径(<em>D</em>)之间存在极显著的回归关系,叶片(<em>W<sub>L</sub></em>)、树干(<em>W<sub>S</sub></em>)、根系和分枝基部(<em>W<sub>B</sub></em>)及植株总生物量(<em>W<sub>T</sub></em>)与分枝直径(<em>D</em>)的异速生长方程分别为: <em>W<sub>L</sub></em>=0.187D<sup>1.855</sup>(<em>R</em><sup>2</sup>=0.612,<em>P </em>< 0.0001);<em>W<sub>S</sub></em>=0.267D<sup>1.906</sup>(<em>R</em><sup>2</sup>=0.821,<em>P </em>< 0.0001);<em>W<sub>B</sub></em>=4.6D<sup>1.136</sup>(<em>R</em><sup>2</sup>=0.644,<em>P </em>< 0.0001);<em>W<sub>T</sub></em>=3.614D<sup>1.446</sup>(<em>R</em><sup>2</sup>=0.801,<em>P </em>< 0.0001)。我国不同地区秋茄林地上生物量与林龄和纬度之间存在显著的回归关系:lg(地上生物量)=3.123 + 0.84 × lg(林龄)-2.019 × lg(纬度),(<em>R</em><sup>2</sup>=0.431,<em>F</em><sub>2,11 </sub>=4.161,<em>P </em>=0.045)。秋茄种群生物量随着林龄的增加而增加,随着纬度的升高呈现降低趋势。浙江鳌江河口3年、5年和10年龄人工秋茄林生物量分别为7.13、11.32和24.35 t/hm<sup>2</sup>,其中5年龄秋茄林生物量仅为广东湛江同龄秋茄林(自然湿地生境)生物量的18%。然而,广东深圳的3年龄秋茄林(人工湿地生境)生物量仅为该研究中同龄秋茄林生物量的9.3%。此外,以≤11年龄的人工秋茄纯林为对象,建立了种群密度与种群植株平均生物量的关系: lg(平均单株地上生物量)=8.468-2.1 × lg(种群密度),(<em>R</em><sup>2 </sup>=0.961,<em>F</em>=99.764,<em>P </em>=0.001),秋茄种群密度越小,平均植株生物量越大,平均单株生物量较符合Yoda提出的-3/2自疏定律为快,自疏指数为-2.1。因此,纬度和林龄是秋茄种群生物量的主要影响因子,生境类型、种群密度等因素对红树林种群或群落生物量的积累也至关重要。
An assessment method of Kandelia obovata population biomass [J].https://doi.org/10.5846/stxb201105160634 URL Magsci [本文引用: 1] 摘要
采用异速生长方法,建立树干基部多分枝型秋茄生物量与分枝直径的函数模型,根据该模型计算了浙江鳌江河口人工秋茄林生物量,并比较了我国不同地区秋茄林生物量差异。结果表明,秋茄生物量(<em>W</em>)与分枝直径(<em>D</em>)之间存在极显著的回归关系,叶片(<em>W<sub>L</sub></em>)、树干(<em>W<sub>S</sub></em>)、根系和分枝基部(<em>W<sub>B</sub></em>)及植株总生物量(<em>W<sub>T</sub></em>)与分枝直径(<em>D</em>)的异速生长方程分别为: <em>W<sub>L</sub></em>=0.187D<sup>1.855</sup>(<em>R</em><sup>2</sup>=0.612,<em>P </em>< 0.0001);<em>W<sub>S</sub></em>=0.267D<sup>1.906</sup>(<em>R</em><sup>2</sup>=0.821,<em>P </em>< 0.0001);<em>W<sub>B</sub></em>=4.6D<sup>1.136</sup>(<em>R</em><sup>2</sup>=0.644,<em>P </em>< 0.0001);<em>W<sub>T</sub></em>=3.614D<sup>1.446</sup>(<em>R</em><sup>2</sup>=0.801,<em>P </em>< 0.0001)。我国不同地区秋茄林地上生物量与林龄和纬度之间存在显著的回归关系:lg(地上生物量)=3.123 + 0.84 × lg(林龄)-2.019 × lg(纬度),(<em>R</em><sup>2</sup>=0.431,<em>F</em><sub>2,11 </sub>=4.161,<em>P </em>=0.045)。秋茄种群生物量随着林龄的增加而增加,随着纬度的升高呈现降低趋势。浙江鳌江河口3年、5年和10年龄人工秋茄林生物量分别为7.13、11.32和24.35 t/hm<sup>2</sup>,其中5年龄秋茄林生物量仅为广东湛江同龄秋茄林(自然湿地生境)生物量的18%。然而,广东深圳的3年龄秋茄林(人工湿地生境)生物量仅为该研究中同龄秋茄林生物量的9.3%。此外,以≤11年龄的人工秋茄纯林为对象,建立了种群密度与种群植株平均生物量的关系: lg(平均单株地上生物量)=8.468-2.1 × lg(种群密度),(<em>R</em><sup>2 </sup>=0.961,<em>F</em>=99.764,<em>P </em>=0.001),秋茄种群密度越小,平均植株生物量越大,平均单株生物量较符合Yoda提出的-3/2自疏定律为快,自疏指数为-2.1。因此,纬度和林龄是秋茄种群生物量的主要影响因子,生境类型、种群密度等因素对红树林种群或群落生物量的积累也至关重要。
|

/
| 〈 |
|
〉 |